4. Colour in Fractions

• Colour in Fractions Activity Sheet: pptx PDF
• Two dice for each group of students - one labelled 1, 2, 2, 3, 3, 4 and the other labelled */2, */3, */4, */6, */4, */12 (nets available here: docx PDF)
• Coloured pencils or markers

This stage has been inspired by the ‘Colour in fractions’ problem published by Clarke and Roche (2014), and is reproduced with permission.

The purpose of this game is for students to see that fractions can be represented in multiple ways. Students will consolidate their understanding of the size of fractions, equivalent fractions and they will be introduced to improper fractions.

Introduce the game of ‘Colour in Fractions’, which students will play in pairs. Provide each student with a Colour In Fractions activity sheet (available in Materials and texts) or a black and white fraction wall. Provide each pair of students with the two dice.

Display an interactive fraction wall or an enlarged fraction wall that is easily visible to all students.

Students may have already seen a fraction wall however it is worth explaining how it is made up. It consists of different fractions from one whole to twelfths, with each horizontal strip of the wall representing one whole.

Explain that students should record their data in the ‘What I rolled’ and ‘What I shaded’ sections of the worksheet. This may be useful as a discussion point later.

Model the game to the class by inviting a student to play a few rounds against you.

1. Invite the student to roll both dice to create a fraction. For example, a 3 and */4, would create ³/₄.

2. Ask the student to shade the fraction on their wall. An obvious option for this student may be to colour in three quarters of the ‘quarters’ strip of the wall. However, emphasise to students that they can shade any fraction of the wall that is equivalent to ³/₄. They are not limited to the quarters strip of the fraction wall just because that was the fraction rolled.

At this point, prompt the class to refer to their fraction wall to consider other options they could shade in. They may come up with ⁶/₈ or ⁹/₁₂. Ask students if they can identify any possibilities where they can combine parts of two different strips. They may see that ²/₃ together with ¹/₁₂ will also make up ³/₄. In other words, they are adding the two fractions together: ²/₃ + ¹/₁₂, which equals ³/₄.

Considering other options to make the fraction rolled is an important part of the game. Through this process, students will notice equivalent fractions, particularly involving more difficult fractions. They may also notice how combinations of different fractions can also produce an equivalent fraction for the one they rolled.

3. Ask the student to fill in the first row of the ‘What I rolled’ and ‘What I shaded’ columns on their activity sheet. Remind students to record the fractions they combined to make an equivalent fraction in the 'What I shaded' column where appropriate.

4. As the second player, model your first turn at the game, by rolling the two dice, forming a fraction, colouring that fraction on the fraction wall, and completing the relevant row on the activity sheet.

5. Take turns rolling the dice, forming fractions, colouring that fraction on the fraction wall, and filling in the next row of the ‘What I rolled’ and ‘What I shaded’ columns on the activity sheet.

6. Explain to the class that the winner will be the first person to completely shade in their fraction wall.

To win, the player must roll the exact fraction required to complete their fraction wall. If they don’t roll the exact fraction required, the game continues. If the game is not completed, then the winner will be the person who has shaded more of their fraction wall.

During the demonstration of the game begin with easier fractions. So, if the student rolls a difficult fraction or one that creates an improper fraction then ask them to roll again until a more accessible fraction is created.

Other rules of the game:

• Players cannot shade only part of a ‘brick’. While they can use bricks from multiple strips, they must be entire bricks.
• Strips do not have to be coloured from left to right.
• Use a different colour for each roll so both players can confirm that what they shaded matched the fraction rolled.
• If a player is unable to colour in a new fraction or fractions, they can pass.

1. Students play the game in pairs to explore equivalent fractions

Once the demonstration is complete, ask each pair to play the game.

Encourage the use of correct mathematical language as students play and create their fractions. For example, ¾ should be read as three quarters not three over four or three out of four. This will help address the misconception that a fraction is not like other numbers.

Enable students by encouraging the pair to work on the same fraction wall together. This may help build confidence and understanding until they can confidently play the game on their own. Providing students with a simplified fraction wall with the more complex denominators removed can also enable student participation.

Alternatively, provide students with two copies of the fraction wall. One is blank while on the second the bricks are individually labelled then cut out so that the students can physically manipulate the pieces to find equivalent fractions.

Extend students by providing a fraction wall with more strips (denominators). For example, include fifths and sevenths. Increase the complexity by including strips with larger denominator values such as fifteenths or twentieths.

Once the game is over, ask students to share one of their most interesting turns so that all students are exposed to the many different strategies that can be used during this game. Which of these strategies would give you a greater chance of winning the game? Discuss why they think so.

To maximise the impact of this game on student learning and understanding it is recommended that the game be played a few times. Every time students play the game, they will explore new strategies and further develop their understanding of fractions.

2. Exploring improper fractions

While there has been no mention of creating improper fractions, these will certainly occur during the game, given the way the dice have been labelled. Rather than explain the improper fractions to the students, observe how students deal with them as they occur. If students have a good understanding of the meaning of the denominator and numerator, then they should be able to determine what the improper fraction means.

Address incorrect language, such as naming the fraction ³/₂ as three twos, which may indicate a lack of understanding of the meaning of the denominator (size of the part) and numerator (the number of parts of that size). Students need to understand that ³/₂ means that the size of the parts is halves and in this case there are 3 of those halves, so the fraction is three halves. In this case the fraction could also be written as 1 ¹/₂.

Ensure that all students develop the understanding that fractions lie between each adjacent integer, not just zero and one.

Understanding the meaning of an improper fraction will help students recognise that they are a useful tool in winning the game, as they allow more bricks to be shaded in a single turn.

Conduct a mini-lesson to enable students who are experiencing difficulties understanding improper fractions. For example, you could use pattern blocks, such as a hexagon and a trapezium, to model improper fractions:

If the hexagon represents one whole, what fraction of the hexagon is the trapezium? Students should see that the trapezium is half of the hexagon. Therefore, by combining these shapes we see that we have one whole and one half which can be written as 1 ¹/₂.

If we replace the entire hexagon with two trapeziums, what fraction is represented by the three trapeziums? 

This diagram is now showing three halves which can be written as ³/₂. Highlight to the students that the fraction for this diagram can be written in different ways, either 1 ¹/₂ or ³/₂, which means these notations must be equal. Repeat this with different improper fractions until students are confident with this concept.

3. Adding and subtracting fractions

While playing this game students are encouraged to look at multiple ways of representing fractions. One of those includes using bricks from multiple strips within the fraction wall.

For example, if a student rolls ²/₃, this could also be represented by ⁴/₈ + ²/₁₂. From the fraction wall below we can see that if I combine the four eighths and the two twelfths into one strip this is the same as the two-thirds strip.

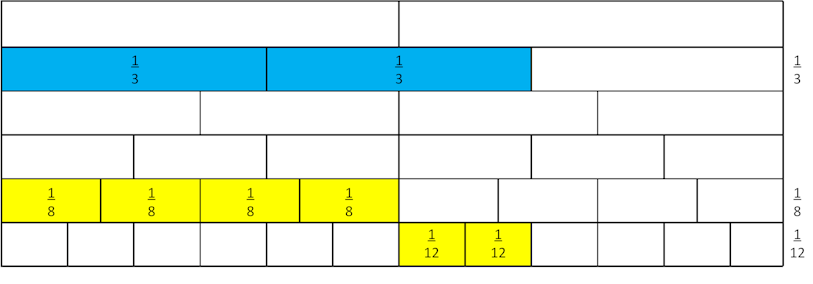
This introduces the concept of adding fractions. Ask a student who used one of these strategies to share why their combination worked. Did they notice any patterns in this combination of fractions?

How many different number sentences can you write to equal the length of one strip, that is, 1? For example, one number sentence is ²/₃ + ¹/₆ + ²/₁₂ = 1. Ask students to think about the relationship between the fractions.

If the fraction wall is fully shaded, what will the parts add up to? Ask each student to write down one way of showing this.

Use the fraction wall to show subtraction of fractions with the same denominator.

What fraction of the wall is shaded? Students should be able to see that ⁶/₈ is shaded.

If we took away four of these, what fraction remains? (i.e. ⁶/₈-⁴/₈) Students can see from the strip that ²/₈ remain.

Using their fraction wall, ask students to come up with as number sentences as they can involving adding and/or subtracting fractions.

Areas for Further Exploration

1. Adding fractions with unlike denominators

While adding fractions with unlike denominators is beyond the Level 5 curriculum, some students may be ready for this challenge.

When adding fractions with different denominators, another method is to use an area model.

For example, if we wanted to add ²/₃ and ¹/₅, we could use an area model.

Begin with two equal sized rectangles. Divide one rectangle into thirds and another into fifths and shade the relevant fractions.

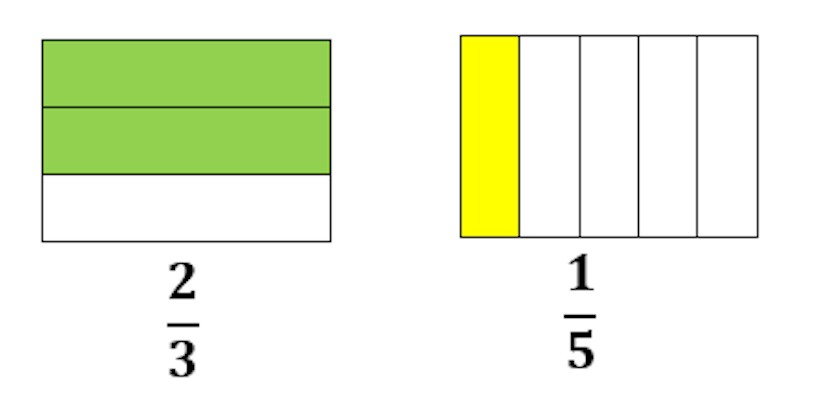
Discuss why adding these two fractions together is difficult. Students should recognise that the parts of the fractions of each rectangle are not the same and so they cannot just add them together yet. Using an area model or other manipulative allows students to use reasoning to see that they will need to find a model that will represent both thirds and fifths.

Ask students to divide the rectangles so that both thirds and fifths are represented. They may need prompting to see that dividing the thirds rectangle further by fifths and the fifths rectangle by thirds, will create two rectangles with the same number of squares. The two rectangles have now been divided into fifteen equal squares.

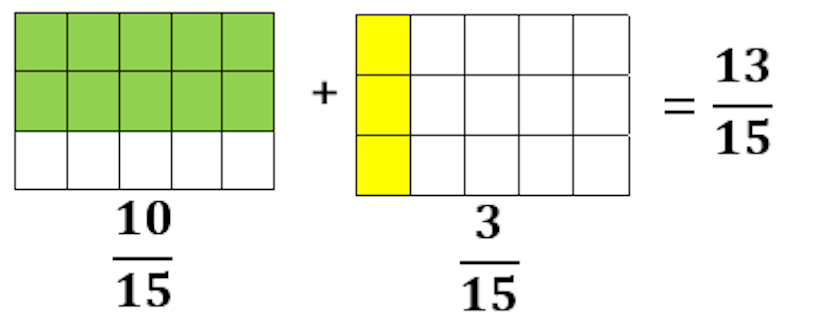
It is important for students to understand that each rectangle has now been divided into 15 equal parts or fifteenths. Since both rectangles now have equal parts, the total number of shaded squares can be determined. This model is now representing both thirds and fifths.

2. Probability

The game could lead to further discussions and applications involving probability. For example, with two eighths left to win the game, what is the chance that I will roll this exact fraction? Ask students to think about how they may work this out.

Encourage students to formulate and test their ideas. Providing a table where they can write all the possibilities may be helpful as students will be able to see that there are 36 possible rolls in total. The fraction ²/₈ appears twice in the table so the chance of rolling ²/₈ is two out of a possible 36 rolls.

Students may also realise that ²/₈ is equivalent to ¹/₄. What is the chance of rolling ¹/₄? If they can win by rolling ²/₈ or ¹/₄, do they have a better chance of rolling what they need to win? What is the chance of rolling either ²/₈ or ¹/₄?

Some students may not be at the level of working out probability values, but you could still facilitate a discussion around the language of probability such as the likelihood of a fraction coming up or the chance of winning the game and so on.

“Colour in Fractions” exposes students to the concepts of equivalent fractions and adding fractions which you may wish to review and consolidate with students. A strong understanding of fraction equivalence will assist students with fraction computations.

1. Equivalent fractions

One of the main aspects of fractions addressed in this game is the notion of equivalent fractions.

To consolidate student understanding of equivalent fractions, provide opportunities for students to use different models (e.g. pattern blocks, grid paper, set models and number lines) to answer a variety of questions relating to equivalent fractions. For example:

• How many different ways can you find to write ²/₈?
• What are equivalent fractions for ⁴/₁₂?
• How else could you write ³/₄?

Allow students to choose the model that helps them most. For example, they may use a fraction wall or pattern blocks to help them visualise the different fractions.

Ask students to submit their answers to assess their understanding.

2. Adding and subtracting fractions

There are many visual representations to help students understand how to add fractions. Begin with adding fractions with the same denominator. Using concrete materials is important here as a visual representation of the fractions.

For example, to add ³/₅ and ¹/₅ the model used here will be fraction tiles. We take 5 tiles each representing one fifth. We turn three of them over (now yellow) to represent ³/₅. We then take another 5 tiles and turn over one tile to represent ¹/₅. How many yellow tiles are there?

The same technique can be used to subtract fractions with the same denominator. If we have 7 tiles each representing one seventh and 5 of them are turned over, what fraction do we have? Students should see the fraction is ⁵/₇. If we then take away two of these tiles (turning them back over to the blue side) what fraction is left? To make this easier for students to visualise, it may be helpful to use tiles with the fraction labels on them.

Provide different examples requiring students to either add or subtract fractions and check student understanding by observing them manipulating set models or any other chosen model.

To check student understanding of adding and subtracting fractions, provide open questions where students can set their own level of challenge. For example, write at least 10 different number sentences, using fractions, that equal 1. Encourage students to write number sentences showing both addition and subtraction. To make this more challenging ask students to write number sentences that equal 2 or ³/₄.

The teaching idea Cuisenaire rods from the Mathematics Curriculum Companion provides another tool for adding and subtracting fractions.

Australian Association of Mathematics Teachers, n.d. Colour in Fractions game board. [Online]
Available at: topdrawer.aamt.edu.au/content/download/20285/275521/file/tdt_F_colourinfractionsgameboard.pdf
[Accessed 15 March 2022].

Clarke, D. & Roche, A., 2014. Engaging Maths: 25 Favourite Lessons. 2nd Edition ed. Melbourne: Mathematics Teaching and Learning Centre.

Educational Computing Support Services, n.d. Fraction Wall Games. [Online]
Available at: www.numeracyhelper.com/fractionwalls/
[Accessed 15 March 2022].

State of Victoria (Department of Education and Training), 2019. Addition and Subtraction of Fractions. [Online]
Available at: fuse.education.vic.gov.au/MCC/CurriculumItem?code=VCMNA188
[Accessed 15 March 2022].

Visnos Mathematics, 2019. Fraction Wall. [Online]
Available at: www.visnos.com/demos/fraction-wall
[Accessed 15 March 2022].