3. Daniel's Great Flight

• Daniel’s great flight – Scenario cards: docx PDF

The film Up (Disney and Pixar, 2009), includes a scene of an elderly man escaping by attaching multitudes of helium balloons to his house, enabling it to lift into the air.

In 2015, Daniel Boria, a 26-year-old Canadian completed a similar stunt in real life, attaching over 100 helium balloons to a lawn chair, enabling him to 'fly' over the city of Calgary.

Share this story and concept (using multiple balloons to rise high in the air) to set the context for this activity. The movement of the chair can be used to introduce the concepts of positive and negative numbers, and their relative position on a number line.

If you want to show videos to your class, Up's flying house is available here and a video of Daniel in the air is available here.

After familiarising students with the story, draw a vertical number line on the board, starting at zero, with numbers going upwards. Draw a chair aligned with the number zero. It is important that students recognise zero as an actual number that has a position on a number line.

Ask students to imagine that each balloon will make the chair rise by one metre.

Model some movement of the chair for students. For example, tying three balloons to the chair will raise it to a height of 3 metres.

Prompt discussion from students about strategies that Daniel may have used to return to the ground. Guide students to the recognition that by either removing some balloons, or, making his chair heavier somehow, Daniel would have been able to make his chair come back to Earth.

1. Introduce the idea of adding weights to the bottom of Daniel’s chair to change the position of the chair.

Ask students to imagine that adding weights act as a counterbalance to the balloons. While each balloon makes the chair rise by one metre, each weight brings the chair down by one metre. Alternatively, suggest that a number of seagulls, conveniently each the same weight as a large helium balloon, have taken interest in Daniel’s adventures, and choose to land on his chair.

Model some further movements of the chair on the board. Discuss where the chair would move to if balloons were added, and then if birds landed on the chair.

Facilitate a discussion with students about how the number line may be extended to include negative numbers within this context. Edit the number line on the board to include negative numbers. Students could imagine the chair going underground, into a large cave or mine shaft, or off the edge of a cliff.

This is one context through which negative numbers, and their position on a number line, can be introduced to students. Other common contexts to introduce negative numbers involve temperature scales, money, golf scores (relative to par), and stairs or elevators going underground into basements and carparks. Select contexts that are familiar to the students in your class when introducing negative numbers.

Use the scenario cards to present students with the details of ‘Daniel’s first journey’ (available in Materials and Texts). Print and share these with students, or project this onto the whiteboard or screen.

Ask students to use the details of his flight to describe the position of Daniel’s chair after each part of the journey. Students may use phrases such as ‘five metres above the ground’ or numbers such as ‘2’ to describe the position of the chair.

Enable students by providing them with an individual number line, incorporating both positive and negative numbers, and a visual aid to represent the chair (a counter, or block). You could also use tape to create a number line on your classroom wall or floor and ask students to act out the movement of the chair.

You could alter the context in which students are working with negative numbers to something more familiar to them, using some of the different contexts listed above as ideas.

2. Introduce the idea of taking away balloons, or taking away weights, to change the position of the chair.

Develop student understanding of this concept by posing questions such as:

• ‘What would happen to the position of the chair if I took away 3 balloons?’
• ‘What would happen to the position of the chair if I took away 6 weights?’

Students model these possibilities on the number line and to explore ideas through discussion.

Provide students with opportunities to recognise and explain that taking away balloons will make the chair move down and taking away weights will make the chair move up.

Model some further movement of the chair on the board and guide students to the understanding that taking away one weight will have the same effect on the chair’s height as adding one balloon. Discuss where the chair would move to if balloons were taken away, or weights were taken away.

Present students with the scenario card for ‘Daniel’s second journey’ (see Materials and Texts) and ask students to describe the position of Daniel’s chair after each part of the journey.

Provide further opportunities for students to explore the movement of the chair across a range of positive and negative values by presenting them with the scenario cards for ‘Daniel visits your school’. 

Areas for further exploration

1. Addition and subtraction of integers

The movement of the chair via the addition and subtraction of both balloons and weights provides a contextual introduction to the addition and subtraction of both positive and negative numbers.

Use the descriptions on the first scenario card as a means of provoking student understanding of the concept of the addition of negative numbers. The following exchange is a sample of how this understanding may be drawn out:

Teacher: “After Daniel adds five balloons, he added three weights. What happened to the chair?”

Student: “It went down by three metres, the three weights moved the chair down.”

Student: “Well, the chair was at 5, and went down to 2, so we could write 5 - 3 = 2”

Teacher: “Does that describe what Daniel did to his chair?  We added three weights, so how could we possibly show adding something to 5 and then finishing at 2?”

Supplement this question by writing 5 + ? =2 on the board and indicating that the question mark represents the effect of the three weights.

Student: “Well, each weight moves the chair down by 1, so we could think of a weight as representing the number ‘negative 1’. Three weights could represent ‘negative 3’. So adding three weights to the chair could be written as 5+-3=2”.

Explain that we could also put a bracket around the -3 to make it clear that it is a number in its own right, so we can write this as 5+(-3)=2.

Teacher: “OK, so what could say in general happens when we add a negative number to something?”

Student: “Adding a negative number is like subtraction. It makes something smaller”.

Invite students to write mathematical statements for the remainder of the movements described on the first scenario card.

Use a similar strategy to introduce the concept of subtraction of negative numbers within this context. The following exchange is a sample of how this understanding may be drawn out:

Teacher: “Imagine Daniel’s chair was floating, four metres above the ground, with some balloons and weights attached to it. What would happen if I took some of the weights away?”

Student: “The chair would move upwards, there’s not as many weights dragging it down now.”

Teacher: “OK, so what if I removed five weights?  How could I write this as a mathematical statement?”

Student: “The chair would go up to nine metres, so we could write 4 + 5 = 9”.

Teacher: “You’re right, it would go up to nine metres, but I didn’t add anything to the chair, I took away five weights. How could I show this in my mathematical statement?”

Supplement this question by writing 4 - ? = 9 on the board.

Student: “Well, like we said before, each weight could represent negative 1, so five weights could be represented by the number negative 5. We could say that 4 - (-5) = 9”.

Teacher: “Great! So what happens when we subtract a negative number from something?”

Student: “It makes something bigger. Subtracting a negative number is like adding a positive number”.

2. Multiplication of integers

Introduce the idea of ‘super balloons’ and ‘super weights’, which can move the chair by different amounts.

Start by relating the size of these to the original balloons and weights.  For example, a “5 balloon” is 5 times stronger than a normal balloon, and a “3 weight” is three times stronger than a normal weight.

Provide students with a range of scenarios using multiples of these super balloons and super weights and ask students to describe the position of the chair or write equations that represent the movement.

For example (sample student responses written in red):

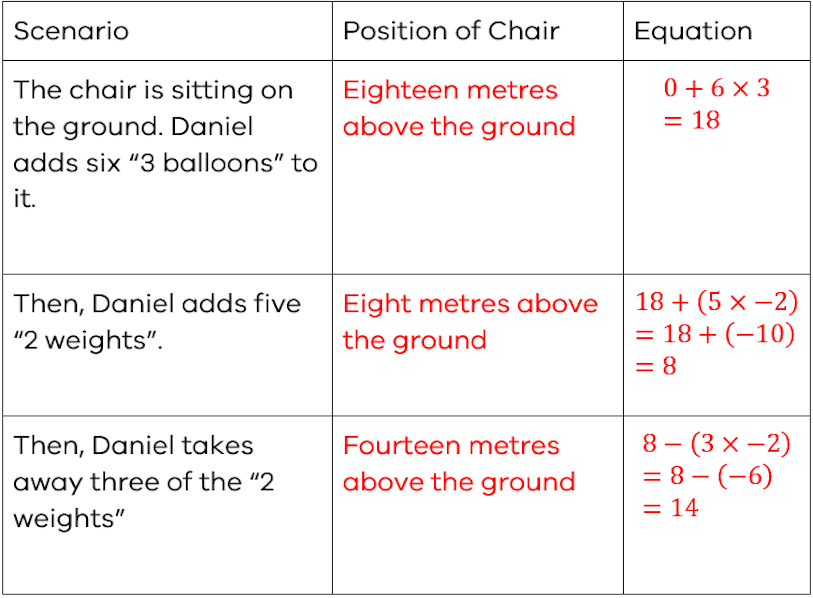
This stage exposes students to the relative position and size of positive and negative numbers, relative to one another, and to zero. Opportunities are also provided to introduce the concepts of addition, subtraction, and multiplication of integers.  Consider the progress made by students when determining which skills and concepts you select to review.

Two suggested concepts for review are presented below.

1. Negative numbers are used to represent values that are smaller than zero

You may wish to emphasise the following concepts:

• the use of language such as ‘negative three’ rather than ‘minus three’ allows us to describe the position and size of a value instead of describing an operator
• we use specific notation to represent a negative number. The value ‘negative three’ can be written as -3. We may write a negative number in a bracket to emphasise the value of the number. For example, negative 12 can be written as (-12)
• negative numbers are located to the left of zero, or below zero, on a number line. This activity used vertical number lines due to the context; exposing students to a range of number lines, both horizontal and vertical, will help consolidate their understanding of the position and size of negative numbers
• negative fractions and decimals are also numbers that have a relative position on a number line. Contexts such as temperature and money are useful for exploring the size of negative rational numbers
• pairs of numbers such as two and negative two, and eight and negative eight, can be thought of as ‘opposites’ and are equal distance from zero
• negative numbers that are closer to zero (such as negative four) are larger than negative numbers that are further from zero (such as negative twelve). The use of a number line can be very useful to help emphasise this point.

You could support students to consolidate their understanding of negative numbers by:

• providing the opportunity to complete the directed number activities developed by reSolve (a collaborative project between the Australian Academy of Science and the Australian Association of Mathematics Teachers). These provide additional opportunities, in different contexts, for students to work with negative numbers.
• asking students to construct a personal timeline with key events that happened before they were born (e.g. the birth of an older sibling) or after they were born (e.g. the move to a new house). With zero representing the date of their birth, students could assign key events a numeric value (such as -3 for a sibling born three years before the student’s date of birth).

Extend students by suggesting they partition years into seasons or months, to gain further exposure to fractional values, both positive and negative.

You could ask students to submit the timeline as a means of assessing student understanding of positive and negative numbers and their relative sizes and positions.

2. We can use recognisable patterns to help us add and subtract integers

You may wish to emphasise the following concepts:

• We use the word integers to describe all positive and negative whole numbers, as well as zero.
• Adding a negative number to a quantity has the same effect as subtracting a positive number; this was seen in the task by the addition of weights moving the chair down.
• Subtracting a negative number from a quantity has the same effect as adding a positive number; this was seen in the task by the subtraction of weights moving the chair up.
• ‘Opposite pairs’ of numbers such as five and negative five will always add to zero; this can be shown as 5 + -5 = 0 or 5 + (-5) = 0.

Support students to consolidate their understanding by providing further practice of addition and subtraction of integers. Sample practice questions within a range of contexts are provided below. You could ask students to write and evaluate mathematical expressions for these contexts.

a) Last weekend I played in a golf tournament. For my two rounds, my scores were -4 and +3. What was my overall score for the tournament? Alternatively, you may like to provide the final score for the golfer and ask students to nominate possible scores for the individual rounds.

b) In Oslo, the temperature was -4 degrees, and then dropped a further 6 degrees. What was the temperature then?

To promote relevance and personal connection, you may like to select towns or cities that the students are familiar with and ask them to construct a reasonable scenario involving temperature change in that city. Alternatively, to promote geographical awareness, students could be asked to research four cities around the world that experience both positive and negative temperatures and write a problem for each city. Other students could then use their own geographical knowledge to try and match the problem to the city, using skills of reasoning and justification.

c) Provide students with an equation (such as 7 + -4 = 3) and ask them to develop their own ‘story’ that the equation could represent.

You may like to read Reading and discussing operations for meaning from the Literacy in Mathematics section of the Literacy Teaching Toolkit, to support you in scaffolding students to understand how to use various operators when working with both positive and negative numbers.

Australian Academy of Science, 2018. Directed Number. [Online]
Available at: https://www.resolve.edu.au/directed-number
[Accessed 15 March 2022].

BBC News, 2015. Canadian flew over Calgary in chair carried by balloons, 2015, BBC News, 6 July. [Online]
Available at: www.bbc.com/news/world-us-canada-33414264
[Accessed 15 March 2022].